A Practical Test for the Central Effect Principle
Gravitation Metrics and Hydrogen Atom
by Michael George
If the Central Effect Principle was to have universality, it must – according to the Principle of Analogy – apply for the Cosmos as a whole as well as to all its subunits, for galaxies, solar systems and planets right down to the atom.
So far there is no unified theoretical description of the largest and the smallest. In modern science one got used to divide cognisance: For the macrocosm the general theory of relativity was competent, for the microcosms, however, the quantum theory.
As the general theory of relativity is no longer compatible with quantum theory, there is an enormous gap between the image of the macrocosms and that of the microcosms. More precisely: The microcosms cannot be described with the general theory of relativity, and the realisations from quantum theory concerning the microcosms lead to a cosmological picture that is not compatible with the interpretations of general relativity.
Let us find out whether we may close this gap. Object of our consideration shall be a hydrogen atom (H). In the periodic table of the elements the H-atom is the simplest atom. It is made up of a nucleus, the proton, and a rotating satellite “shell”, the electron. In the classical concept electrically the nucleus is positively, the electron negatively charged.
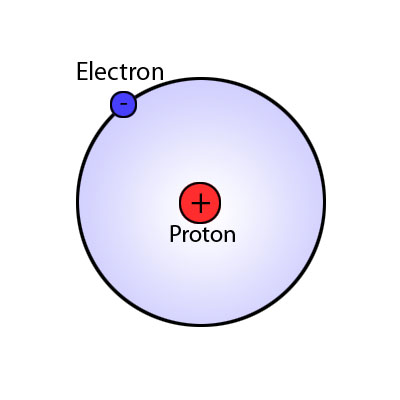
The hydrogen atom is the smallest system with a centre and a satellite that we know. If such an atom is in a state of relative rest in relation to the Earth’s surface and is “left to itself”, the rotating shell – the electron – is in the basic state. This means that the electron takes on a distinctive “orbit”, being the “lowest”, the relatively closest to the proton.
Is the electron now “excited” by being “hit” of light energy (photons), it can jump to the next-higher (next-outward) orbit. But for this there are exactly determined prerequisites. The electron cannot change to arbitrary orbits.
Every possible orbit represents a defined energy level, and when the electron shall go to the second orbit – as counted from the centre – a defined amount of electric energy is needed to make this jump possible. This amount of energy may also be called an energy quantum. For this reason, the “allowed” electron orbits are called quantum orbits that from the inside out are named n = 1, n = 2, n = 3 etc.
The characteristic result is now that the exciting energy for the “quantum leap” of the electron must be kept the lower the larger the orbit is that it at the moment occupies.
Stated differently: The higher the excitement state of the electron, the smaller is the energy necessary for a further orbit jump. This also means that the energy an electron carries is higher the further away it is placed. This context is shown in the following table (energy increase in electron volt eV):
| Main Quantum Number n | Energy Increase to n = 1 (eV) |
|---|---|
| 1 | – |
| 2 | 10,15 |
| 3 | 12,03 |
| 4 | 12,68 |
| 5 | 12,99 |
Let us see now what amount of energy is needed to bring the electron from n = 1 (basic state) to n = 2, from n = 2 to n = 3 etc. (referred to n = 0):
| Main Quantum Number n | Energy Increase to n=1 (eV) | Energy Requirement (eV) |
|---|---|---|
| 1 | – | 13,53 |
| 2 | 10,15 | 3,38 |
| 3 | 12,03 | 1,5 |
| 4 | 12,68 | 0,85 |
| 5 | 12,99 | 0,54 |
Let us remember how we approached the question quantum orbits. If the Central Effect Principle should have universal validity, it must also be applicable to the hydrogen atom and to the stimulative behaviour of the electron. So the proton – more exactly: the centre of the proton – should be the singular source of a gravitation field, and the electron would then be the smallest natural satellite in the smallest natural gravitation field.
Accordingly should the inertia or contumacy of the electron against an alteration of movement (an orbital or quantum leap) should drop with the square of the orbital radius or proportional to the enlargement of its spherical energy area.
This idea does not appear in nuclear physics. For the Coulomb’s Law that is valid there demands the “force-free” rotation of the electron. This law is identical to Newton’s Third Law. Here, too, the “centrifugal force” of the electron annuls the “attractive” effect of the protons.
Now we have seen in the large scale that the presumption of a gravitational force in natural gravitation fields is untenable. As we showed, it would then be necessary to postulate that all natural orbit or rotation movement occur force-free. Accordingly there cannot be any force in Nature that causes the rotation or orbit movements of satellites, because centrifugal force and gravitation cancel each other out.
This assumption is highly unsatisfactory, and it is one of the curiosities of intellectual history that even the most important minds after Newton would be satisfied with this “black hole of thinking”. The only thinker of the last three hundred years who doubted this stipulation was Ernst Mach. His principle shows in a pellucid fashion that no satellite can be without acceleration.
Mach, however, correlated his principle only to “static” straight force connections and not to rotating systems. The Central Effect Principle in contrast shows that the straight “force connection” was a fiction stemming from mechanistic thinking.
All natural movement follows a curvilinear track, and all natural movement is accelerated movement. Except for Mach’s principle only the Central Effect Principle contains the basic tenet that there cannot be any force-free movement.
We must therefore exclude that the electron travels on force-free orbits. What results may we expect? First of all the inertia of the electron must – as indicated above – sink with an orbital space in the ration of 1 : r².
One would then also expect that in the basic state (n = 1) the relatively highest energy input would be required to overcome the contumacy of the electron against a change of orbit to n = 2. With the double distance the contumacy would have to sink to a quarter of the value that is needed for n = 1.
If we set the needed energy input for n = 1 in relation to the orbits that follow outwards, the following picture emerges:
| Quantum Orbit n | Energy Input (eV) | Ratio | Inertia | Energy Area |
|---|---|---|---|---|
| 1 | 13,53 | 1/1 | 1/1 | 1 |
| 2 | 3,38 | 1/4 | 1/4 | 4 = 2² |
| 3 | 1,5 | 1/9 | 1/9 | 9 = 3² |
| 4 | 0,85 | 1/15,9 | 1/16 | 16 = 4² |
| 5 | 0,54 | 1/25 | 1/25 | 25 = 5² |
The table confirms our expectation completely: The energy requirement of the electron diminishes from track to track exactly following the metric of a gravitation field. In the fifth track the contumacy of the electron is lower than the original state by a factor of 25, and therefore the necessary initiation energy in the fifth track is also smaller by the factor 25 compared to the first track.
The track numbers n are identical with the whole-number multiples of the track distance to the proton. The tracks can also be called inertia steps of the electron. Every inertia step corresponds to a rotating energy plane. Thus the electron may be regarded as a spherical energy plane whose inertia diminishes in the reverse ratio to its size.
In this way we come to the result that the energy of the electron does not increase with an increasing orbit radius as one must suppose when applying Coulomb’s Law. For the contumacy or inertia of the electron decreases outwards in the same ratio as its electric energy increases.
The total energy of the electron is the same in all track states!
| Quantum orbit n | Increase of electric energy relative to the next inner orbit |
Reduction of inertia relative to Track 1 (in brackets relative to the next inner orbit) |
|
|---|---|---|---|
| 2 | 1 : 4 = -75 % | ||
| 3 | Factor 1.185 = + 15.6 % | 1 : 9 = -88.9 % (- 15.6 %) | |
| 4 | Factor 1.054 = + 5.1 % | 1 :16 = -93.75 % (- 5.1 %) | |
| 5 | Factor 1.024 = + 2.3 % | 1 : 25 = -96 % (- 2.3 %) | |
| 2-5 total | Factor 1.28 = + 21.86 % | Factor -1.28 = – 21.86 % |
This allows only one solution: namely to attribute the electron a “composite” energy. The total energy of an electron is then made up of “sluggish” and electric energy. It has as a gravitational rotating as well as an electrically oscillating charge component the ratio of which shifts outwardly in favour of the electric charge component.
One cannot doubt that an electron may occupy only certain “discrete” orbits that are in a whole-number relation to each other. This recognition would also be applicable to the inertia behaviour of the electron: It can only appear as electrical energy plane of a defined size and a defined inertia, whereby the inertia is inversely proportional to the increase in size of the plane.
The Central Effect Principle may – considering all preliminarity and exemplariness of the presented material – be seen as the only universal theory with which simple motion equations for the behaviour of the macrocosm as well as the microcosm may accurately be described.
Thus we may argue that the hydrogen atom represents the smallest natural gravitation field with the smallest natural satellite. The source of the proton vortex field is then the smallest natural singular centre.
There are two properties of the atom that demand our special attention. At first the inertia of the proton is higher than that of the electron at rest by a factor of 1833.
If following to the analogy principle we apply this ratio of inertia to interplanetary orders of magnitude, we come to the fact that our sun also shows a comparable supremacy towards the planet: Relevant calculations indicate that their gravitation potential is higher by the factor of 1000 than that of all planets combined.
With the analogy principle we now assume that neither a random atom nor our solar system are subject to special laws, and so we may conclude that all rotating systems of the cosmos are dominated by a centre whose gravitational supremacy is marked by a factor that lies between 1000 and around 1800.
As late as the 1980s a mass concentration was hypothesized at the centre of our galaxy with an estimate 30 million times the mass of our sun. According to the analogy principle, however, we must side with those thinkers who assume at the centre of our helical island of worlds a gigantic Black Hole.
So we may assume that the 300 billion suns of our galaxy are dominated by a Black Singularity whose gravitational potential is at least that of 300 billion sun masses multiplied by 1000.
The second hallmark of a proton is the – for human comprehension unimaginable – thermo-nuclear potential harboured in that minute nucleus. If we also apply this property following the analogy principle to the sun and to any other centre, we may conclude that the thermic as well as the gravitational potential of a centre of a system must be intimately connected.
This post is also available in: German
